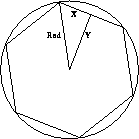
Figure 1: The Garden House
The ria library supports numeric constraints which may involve several variables. Throughout program execution, ria continually narrows the ranges associated with the variables as far as possible based on these constraints. In other words ria supports propagation of intervals, using the range library to record the current ranges, and to detect inconsistencies.
The constraints handled by ria are equations and inequalities between numerical expressions. The expressions can be quite complex, they can include polynomials and trigonometrical functions. This functionality is quite similar to that offered by fd, except that fd can only propagate linear constraints. On the other hand, the finite domain library uses integer arithmetic instead of real number arithmetic, so it is in general more efficient than ria.
We shall confine ourselves here to a single example showing ria at work.
Suppose we wish to build a garden house, whose corners must lie on a given circle. The house should be a regular polygon, but may have any number of sides. It should be as large as possible within these limitations. (Note that the more sides the larger the area covered, until it covers practically the whole of the circle.) However each extra side incurs a fixed cost. The problem is to decide how many sides the garden house should have?
If it had six sides, the house would look as illustrated in figure 1.
The area of the house is 2*6*A where A is the area of the triangle in the illustration. The area of an N-sided house can be modelled in ECLiPSe as shown below.
:- lib(ria).
area(N,Rad,Area) :-
X*>=0, Y*>=0, N*>=3, integers(N),
Rad *>=0, Area*>=0,
Area *=< pi*sqr(Rad),
cos(pi/N) *= Y/Rad,
sqr(Y)+sqr(X) *= sqr(Rad),
Area *= N*X*Y.
cost(N,Rad,W1,W2,Cost) :-
W1*>=1, W2*>=1, Cost *>=0,
area(N,Rad,Area),
Cost *= W1*Area-W2*N.
tcost(N,Cost) :-
cost(N,10,1,10,Cost).
The Area, and Cost-Benefit, of a Garden House
N is the number of sides, and Area is the area of the house.
The variable Rad denotes the radius of the circle, and X and Y
are the lengths of the sides of the
triangle, as illustrated in
figure 1.
ria requires its constraints to be written with a specific
syntax (eg X *>= Y instead of just X >= Y).
This distinguishes ria constraints from linear and finite domain
constraints, which each have their own special syntax.
To work out the payoff between the area and the number of sides, we
define the cost of the house to be W1*Area-W2*N, where W1 and W2
are weighting factors that we can chose to reflect the relative costs
and benefits of the area against the number of sides.
In the model shown in figure  , tcost returns the
cost-benefit of an N-sided house
in case the radius of the circle is 10, and the weights are W1=1
and W2=10.
, tcost returns the
cost-benefit of an N-sided house
in case the radius of the circle is 10, and the weights are W1=1
and W2=10.
We can place this program in a file called house.pl, and then use ECLiPSe to find out some costs by first ``consulting'' the file, as illustrated below, query 1.
[eclipse 1]: [house].
* range loaded
* house.pl compiled
* yes.
[eclipse 2]: tcost(3,C).
* C = C{99.90 .. 99.91}
* yes.
[eclipse 3]: tcost(4,C).
* C = C{159.9 .. 160.0}
* yes
[eclipse 4]: tcost(6,C).
* C = C{199.8 .. 199.9}
* yes.
[eclipse 5]: tcost(7,C).
* C = C{203.6 .. 203.7}
* yes.
[eclipse 6]: tcost(8, C).
* C = C{202.8 .. 202.9}
* yes.
[eclipse 7]: tcost(N,C).
* N = N{3 .. 31}
* C = C{0.0 .. 284.2}
* yes.
[eclipse 8]: tcost(N,C), squash([C],1e-2,lin).
* N = N{3 .. 31}
* C = C{0.0 .. 224.2}
Finding the Optimal Shape for a Garden House
Queries 2-6, above, would seem to indicate
that the seven sided house is best for the given cost
weightings.
However it is also interesting to see whether the interval reasoning system itself can achieve useful propagation without even knowing the number of sides of the house. We show this in query 7.
An upper bound on the number of sides is extracted due to the constraint that the cost-benefit must be positive, but the propagation on the cost-benefit is rather weak. In cases like this, propagation can be augmented by a technique known as squashing, as illustrated in query 8.
We now give two short examples showing limitations of interval reasoning in general. This will motivate the introduction of a linear constraint solver in ECLiPSe, described in section 3.4.
The two limitations are that interval reasoning cannot, even in some quite simple examples, detect inconsistency among the constraints; and in cases where the constraints have only one solution, interval reasoning often fails to reflect this in the results of propagation.
This is illustrated by a couple of simple examples as follows.
[eclipse 1]: lib(ria).
* ria loaded
[eclipse 2]: [X,Y,Z]:: -100.0..100.0,
X+Y *=<1, Z+X*=<1, Y+Z*=<1, X+Y+Z*>=2.
* X = X{-100.1 .. 100.1}
* Y = Y{-100.1 .. 100.1}
* Z = Z{-100.1 .. 100.1}
* yes
[eclipse 3]: [X,Y]:: -100.0 .. 100.0, X+Y *= 2, X-Y *= 0.
* X = X{-98.1 .. 100.1}
* Y = Y{-98.1 .. 100.1}
* yes
Poor Interval Propagation Behaviour
In this case the system failed to detect the
inconsistency in query 2, and did not deduce that only one value
was possible for X and Y in query 3.
The answer is not incorrect, as ria only guarantees that any
possible answers must lie in the intervals returned - it does not
guarantee the existence of an answer in that interval.
Nevertheless it would be useful to have available a more powerful
solver to recognise cases such as these.