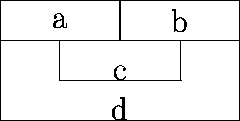
Figure 3: A Simple Map to Colour
As a toy example let us write a program to colour a map so that no two
neighbouring countries have the same colour.
In constraint logic programs, variables start with a capital letter
(eg A), and constants with a small letter (eg red).

Figure 3: A Simple Map to Colour
A generic logic program, in Prolog syntax, that tries find possible ways of colouring this map with only three colours (red, green and blue) is in figure 4.
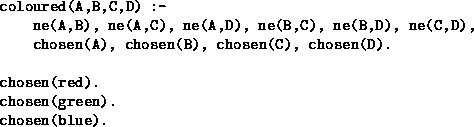
Figure 4: A Generic Logic Program for Map Colouring
In this program the (as yet undefined) predicate ne constrains its arguments to take different values. We will show how different definitions of ne cause the program to behave in different ways.
The predicate chosen can be satisfied in three ways. At runtime the system tries each alternative in turn. If a failure occurs later in the computation, then the alternatives are tried in a last-in first-out basis.
The first definition of ne uses the original disequality of Prolog:
ne(X,Y) :- X\=Y.
If invoked when either of its arguments are uninstantiated variables,
X\=Y simply fails.
To avoid this incorrect behaviour it is possible to
place the constraints after all the choices. In this case the program
correctly detects that there is no possible colouring after checking
all 81 alternatives.
A more efficient Prolog program can be written by interleaving choices
and constraints, but this requires the programmer to think in terms of
the operational behaviour of the program on this particular map.
The same effect can be achieved much more cleanly by using the
program of figure 4 with a new definition:
ne(X,Y) :- X~=Y.
This disequality predicate delays until both arguments have a
fixed value. It then immediately wakes up and fails if both values
are the same.
If the values are different it succeeds.
This program detects that our map cannot be coloured with three
colours after trying only 33 alternatives.
Another disequality constraint is available in CLP, which assumes its
arguments have a finite set of possible values. We can use it by
defining
ne(X,Y) :- X##Y.
This disequality delays until one of its arguments has a fixed value.
This value is then removed from the set of possible values for the
other. To obtain the advantage of X##Y it is necessary to
declare the set of possible values for each variable,
by writing [A,B,C,D]::[red,green,blue].

Figure 5: A Finite Domain CLP Program for Map Colouring
This program detects that the map cannot be coloured after trying only 6 alternatives.
Although this example is so trivial that it is quite simple to solve it in Prolog, the CLP program scales up to complex maps and graphs in a way that is impossible using a programming language without constraints.