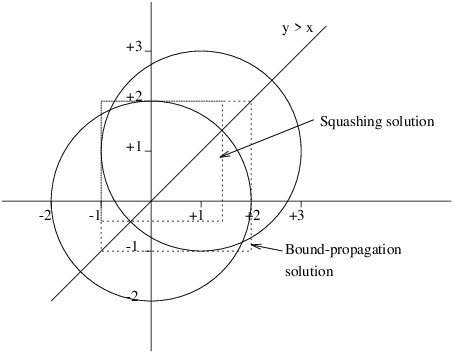
| Figure 3.1: Propagation with Squash algorithm (example) |
Provides a reified form of the ::/2 domain assignment predicate. This reified ::/3 is defined only to work for one variable and only integer variables (unlike ::/2), hence only the Domain formats suitable for integers may be supplied to this predicate.
For a single variable, V, the Bool will be instantiated to 0 if the current domain of V does not intersect with Domain. It will be instantiated to 1 iff the domain of V is wholly contained within Domain. Finally the Boolean will remain an integer variable in the range 0..1 if neither of the above two conditions hold.
Instantiating Bool to 1, will cause the constraint to behave exactly like ::/2. Instantiating Bool to 0 will cause Domain to be excluded from the domain of all the variables in Vars where such an exclusion is representable. If such an integer domain is unrepresentable (e.g. -1.0Inf .. -5, 5..1.0Inf), then a delayed goal will be setup to exclude values when the bounds become sufficiently narrow.
Note that calling the reified form of :: will result in the Variable becoming constrained to be integral, even if Bool is uninstantiated.
Further note that, like other reified predicates, :: can be used infix in an IC expression e.g. B #= (X :: [1..10]) is equivalent to ::(X, [1..10], B). See section 3.2.3 for more information of reified constraints.
Note that the integer forms of the constraints are essentially the same as the general forms, except that they check that all constants are integers and generally constrain all variables and subexpressions to be integral. Thus with integer constraints, the solver does very much behave like a traditional integer solver, with any temporary variables and intermediate results assumed to be integral. This means that it makes little sense to use many of the nonlinear functions available for use in expressions (e.g. sin, cos, ln, exp) in integer constraints. It also means that one should take care using such things as division: X/2 + Y/2 #= 1 and X + Y #= 2 are different constraints, with the former constraining X and Y to be even. That said, if all the constants and variables are integral already and the subexpressions clearly so as a consequence, then the integer (#) constraints and general ($) constraints may be used integerchangeably.
The comparison constraints =:=/2, >=/2, =</2 and
=\=/2 have the same syntax as the standard ECLiPSe built-in
comparison operators (and those of other constraint solvers).
Unless explicitly qualified, the ECLiPSe built-ins are used.
To use these constraints without the need to qualify them, use the
alternative dollar-syntax.
As mentioned earlier, when constraints appear in an expression context, then they evaluate to their reified truth value. Practically this means that the constraints are posted in a passive check but do not propagate mode, whereby no variable domains are modified but checks are made to see if the constraint has become entailed (necessarily true) or dis-entailed (necessarily false).
The simplest and arguably most natural way to reify a constraint is to
place it in an expression context (i.e. on either side of a $=,
$>=, #=, etc.) and assign its truth value to a variable.
For example:
TruthValue #= (X $> 4).
It is also possible to use the 3 argument form of the constraint predicates where the third argument is the reified truth value, for example:
$>(X, 4, TruthValue).
But in general the previous form is recommended as it can be easily
extended to handle the truth values of a combination of constraints, by
using the infix operators and (logical conjunction), or
(logical disjunction) and => (logical implication) or the prefix
operator neg (logical negation). e.g.:
TruthValue #= (X $> 4 and Y $< 6).
Again, as mentioned earlier, there are a number of reified connectives which can be used to combine reified constraints using logical operations on their truth values.
B #= (X $> 3 and X $< 8) or
X $> 3 and X $< 8B #= (X $> 3 or X $< 8) or
X $> 3 or X $< 8B #= (X $> 3 => X $< 8) or
X $> 3 => X $< 8B #= (neg X $> 3) or
neg X $> 3
The logical truth value of a constraint, when reified, can be used to enforce the constraint (or its negation) during search.
The following three examples are equivalent:
X $> 4.
B #= (X $> 4), B=1.
B #= (X $=< 4), B=0.
By unifying the value of the reified truth value, the constraint changes from being passive to being active. Once actively true (or actively false) the constraint will prune domains as though it had been posted as a simple non-reified constraint.
Reified constraints are implemented using the the 3 argument form of the constraint predicate if it exists (and it does exist for the arithmetic relation constraints).
User-defined constraints will be treated as reifiable if they appear in an expression context and as such should provide forms where the last argument is the reified truth value reflected into a variable.
The user-defined constraint should behave as follows depending on the state of the reified variable.
When the reified variable is
unbound, the constraint should not perform any domain reduction on its
arguments, but should check to see if the constraint has become entailed or
dis-entailed, setting the reified variable to 1 or 0
respectively.
In the event that the reified
variable becomes bound to 0 then the constraint should actively
propagate its negation.
In the event that the reified
variable becomes bound to 1 then the constraint should actively
propagate its normal semantics.
These predicates can be used to enumerate solutions to a set of constraints over integer variables. For optimisation, see also the branch_and_bound library.
These predicates can be used to locate real solutions to a set of constraints. They are essentially the same as those that were available in RIA; more details of the algorithms used can be found in section 3.2.10.
These predicates allow one to retrieve various properties of an IC variable (and usually work on ground numbers as well).
With interval constraint propagation, it is sometimes useful to limit propagation for efficiency reasons. In IC, this is controlled by the propagation threshold. The way it works is that for non-integer variables, bounds are only changed if the absolute and relative changes of the bound exceed this threshold (i.e. small changes are suppressed). This means that constraints over real variables are only guaranteed to be consistent up to the current threshold (over and above any normal widening which occurs).
Note that a higher threshold speeds up computations, but reduces precision and may in the extreme case prevent the system from being able to locate individual solutions.
The default threshold is 1e-8.
Some problems can be solved just by interval propagation, for example:
[eclipse 9]: X :: 0.0..100.0, sqr(X) $= 7-X.
X = X{2.1925824014821353 .. 2.1925824127108307}
Delayed goals:
...
yes.
There are two things to note here:
Note that, since variables by default range from minus to plus infinity, we could have written the above example as:
[eclipse 2]: sqr(X) $= 7-X, X $>= 0.
X = X{2.1925824014821353 .. 2.1925824127108307}
Delayed goals:
...
yes.
If too little information is given, the interval propagation may not be able to infer any interesting bounds:
[eclipse 2]: sqr(X) $= 7-X.
X = X{-1.0Inf .. 7.0}
Delayed goals:
...
yes.
There are two methods for further domain reduction. They both rely on search and splitting the domains. There are two parameters to specify how domains are to be split.
The Precision parameter is used to specify the minimum required precision, i.e. the maximum size of the resulting intervals (in either absolute or relative terms). Note that the propagation threshold (section 3.2.8) needs to be one or several orders of magnitude smaller than precision, otherwise the solver may not be able to achieve the required precision.
The lin/log parameter guides the way domains are split. If it is set to lin then the split is in the arithmetic middle. If it is set to log, the split is such as to have roughly the same number of floats to either side of the split. This is to take the logarithmic distribution of the floats into account.
If the ranges of variables at the start of the squashing algorithm are known not to span several orders of magnitude (|max| < 10 * |min|) the somewhat cheaper linear splitting may be used. In general, log splitting is recommended.
A stronger propagation algorithm is also included. This is built upon the normal bound consistency. It guarantees that, if you take any variable and restrict its range to a small domain near one of its bounds, the original bound consistency solver will not find any constraint unsatisfied.

Figure 3.1: Propagation with Squash algorithm (example)
All points (X,Y) Y >= X, lying within the intersection of 2 circles with radius 2, one centred at (0,0) the other at (1,1).
[eclipse 2]: 4 $>= X^2 + Y^2, 4 $>= (X-1)^2+(Y-1)^2, Y $>= X.
Y = Y{-1.0000000000000004 .. 2.0000000000000004}
X = X{-1.0000000000000004 .. 2.0000000000000004}
Delayed goals:
...
yes.
The bound-consistency solution does not take into account the X >= Y constraint. Intuitively this is because it passes through the corners of the box denoting the solution to the problem of simply intersecting the two circles.
[eclipse 2]: 4 $>= X^2 + Y^2, 4 $>= (X-1)^2+(Y-1)^2, Y $>= X,
squash([X,Y], 1e-5, lin).
X = X{-1.0000000000000004 .. 1.4142135999632601}
Y = Y{-0.41421359996326 .. 2.0000000000000004}
Delayed goals:
...
yes.
(Using the facilities described in this section requires importing the ic_kernel module. Also, since they depend on the internals of the IC library, the details presented here are subject to change without notice.)
Often it is difficult to know where the solver spends its time. The library has built-in counters which keep track of the number of times various events occur:
Users who wish to track activity within their own programs may (if they wish) use the same mechanism. New event types can be registered (see below) and actions recorded by calling the ic_event(Event) predicate.
The counters are controlled using the primitives: