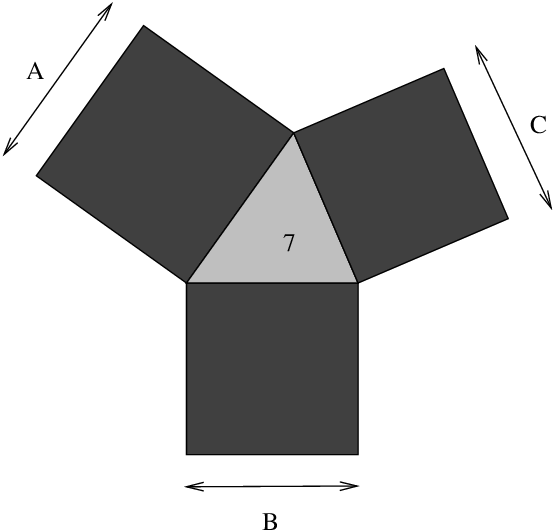
| Figure 9.6: Triangular lake with adjoining square fields |
Consider the following problem:
George is contemplating buying a farm which is a very strange shape, comprising a large triangular lake with a square field on each side. The area of the lake is exactly seven acres, and the area of each field is an exact whole number of acres. Given that information, what is the smallest possible total area of the three fields?
A diagram of the farm is shown in Figure 9.6.

Figure 9.6: Triangular lake with adjoining square fields
This is a problem which mixes both integer and real quantities, and as such is ideal for solving with the IC library. A model for the problem appears below. The farm/4 predicate sets up the constraints between the total area of the farm F and the lengths of the three sides of the lake, A, B and C.
|
A solution to the problem can then be found by first instantiating the area of the farm, and then using locate/2 to find the lengths of the sides of the lakes. Instantiating the area of the farm first ensures that the first solution returned will be the minimal one, since indomain/1 always chooses the smallest possible value first:
|