Figure 2: A Constraint Graph with a Cycle
A key innovation behind constraint programming is constraint propagation. Propagation is a generalisation of data-driven computation. Consider the constraint x = y+1, where x and y are variables. In a constraint program, any assignment to the variable y (eg y=5) causes an assignment to x (x=6). Moreover the very same constraint also works in the other direction: any assignment to x (eg x=3) causes an assignment to y (y=2).
In a graphical application, constraint propagation can be used to maintain constraints between graphical objects when they are moved. For example if one object is constrained to appear on top of another object, and the end-user then moves one of the objects sideways, the other object will move with it as a result of constraint propagation.
In general each object may be involved in many constraints. Consequently the assignment of a new position to a given object as a result of propagation, may propagate further new assignments to other objects, which may cause further propagation in their turn. If each constraint between two object is represented as an edge in a graph, the propagation spreads through the connected components of the graph.
When a particular object is assigned a new position, and the change is propagated from the object to other objects, there is a causal direction. In this case we can assign a direction with each edge of the (connected component of) the graph. As long as the graph is free of cycles, the propagation behaviour is guaranteed to terminate, and produce the same final state irrespective of the order in which constraints are propagated. Efficient algorithms, such as the DeltaBlue algorithm, have been developed for propagation of graphical constraints. They work by firstly generating the directed graph whenever an object is moved, and then compiling this directed graph into highly efficient event-driven code.
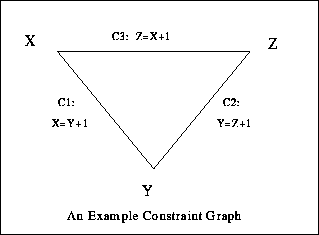
However if the graph contains cycles both these issues arise. Consider, as a simple example, the three constraints C1, C2 and C3 specified thus - C1: x=y+1, C2: y=z+1 and C3: z=x+1.

Figure 2: A Constraint Graph with a Cycle
Assigning y=3 may start a non-terminating sequence of propagations cycling through the constraints C1 (which yields x=4), then C3 (which yields z=5), then C2 (which yields y=6) and then C1 again and so on. Alternatively the same assignment y=3 could propagate through C2 yielding z=2, thence x=1 and y=0 via C3 and C1. In this case the propagation also goes on for ever, but this time the values of the variables decrease on each cycle! Thirdly the same assignment y=3 could yield z=5 via C1 and C3, and z=2 via C2!
In this example the original constraints are, logically, inconsistent. However similar behaviour can occur when the constraints are consistent. In the following example there are constraints on three variables. C4: x+y=z, C5: x-y=z. Suppose the initial (consistent) assignments are x=2,y=0,z=2. Now a new assignment is made to z: z=3. If constraint propagation on C4 yields y=1, then propagation on C5 yields x=4. Now propagation on C4 and C5 can continue for ever, alternately updating y and x.
Propagation algorithms have been developed which can deal with cycles, but if the class of admissible constraints is too general, it is not possible to guarantee that propagation is confluent and terminating.