There already exists a class of modelling languages designed for combinatorial problems. These are the mathematical modelling languages typically used as input to mixed integer programming (MIP) packages. We further discuss MIP, and how to use it through ECLiPSe, in section 3.4 below.
Although the syntax is different, mathematical modelling languages
share many of the features of logic programming.
They support logical variables, and constraints.
They support numerical constraints which, though not supported in
traditional logic programs, are supported by constraint logic programs
as we shall see in the following section.
They support named constraints, which is achieved in constraint logic
programming by introducing a predicate name, eg
precede(T1,T2) :- T1 >= T2.
There are two facilities in constraint logic programming which are not available in mathematical modelling languages. The main one is quite simple: in constraint logic programs it is possible to define a constraint which involves a disjunction. Mathematical programming cannot handle disjunction directly. The second difference is that logic programming allows new constraints to be defined in terms of existing ones, even recursively. In mathematical programming the model is essentially flat, which not only complicates the model but also reduces reuseability within an application and across applications.
To illustrate the advantage of handling disjunction in the modelling language, we take a toy example and present two models: a mathematical programming model and a constraint logic programming model.
Consider the constraint that two tasks sharing a
single resource cannot be done at the same time.
The constraint involves six variables: the start times 
, end times
and resources 
of the two tasks.
The specification of this constraint is as follows:
either the two tasks use distinct resource (First we shall show how it can expressed as a mathematical model without disjunctions. For this purpose it must be encoded using numerical equations and inequalities, together with integer constraints.) or task
ends before task
starts (
) or else task
).
The disjunctions can be captured by introducing three 0/1 variables,
, 
, and 
, and using some large constant, say
100000, larger than any possible values for any of the six variables.
Now we can express the constraint in terms of numerical inequalities as
follows:
If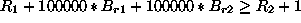
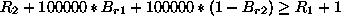
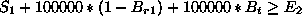
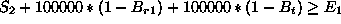
then the two
tasks use different resources.
In this case, if also 
then 
,
otherwise 
and 
.
It is an exercise for the reader to prove that if then the
tasks can overlap.
Otherwise, if 
, then 
entails 
and 
entails 
.
In ECLiPSe this constraint can be modelled directly in logic, as illustrated below.
taskResource(S1,E1,R1,S2,E2,R2) :-
ne(R1,R2).
taskResource(S1,E1,R1,S2,E2,R2) :-
R1=R2, S1 >= E2.
taskResource(S1,E1,R1,S2,E2,R2) :-
R1=R2, S2 >= E1.
Specifying a Resource Contention Constraint in ECLiPSe
We note that the ECLiPSe model is a conceptual model, whilst the mathematical model is a design model. The point here is that in ECLiPSe both models can be expressed, whilst mathematical modelling can only express a design model. Indeed we shall show in section 4.1 below a design model written in ECLiPSe that is very close to the conceptual model.
Another ECLiPSe design model, which is also close to the conceptual model, is handled in ECLiPSe by an automatic translator which builds the MIP model and passes it to the MIP solver of ECLiPSe. This translator is described in [RWH97] which is available from the IC-Parc home page (whose URL is given in section 6 below).
Whilst the above example shows that such complex constraints can be expressed in terms of numerical inequalities, as required for MIP, the encoding is awkward and difficult to debug. It becomes increasingly difficult as the constraints become more complex (eg the current example immediately becomes harder still if the resources have a finite capacity greater than one).
Notice, finally, that the mathematical model requires resources to be identified by numbers, whilst the constraint logic programming model imposes no such restriction as we shall show in section 4 below.