Previous Up

8.9  Exercises

  1. A magic square is a 3 × 3 grid containing the digits 1 through 9 exactly once, such that each row, each column and the two diagonals sum to the same number (15). Write a program to find such magic squares. (You may wish to use the “Send More Money” example in section 8.3 as a starting point.)

    Bonus points if you can add constraints to break the symmetry, so that only the one unique solution is returned.

  2. Fill the circles in the following diagram with the numbers 1 through 19 such that the numbers in each of the 12 lines of 3 circles (6 around the outside, 6 radiating from the centre) sum to 23.

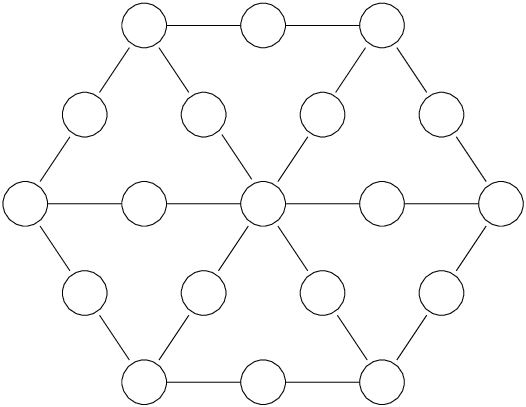
    If the value of the sum is allowed to vary, which values of the sum have solutions, and which do not?

    (Adapted from Puzzle 35 in Dudeney’s “The Canterbury Puzzles”.)

  3. Consider the following code:

    foo(Xs, Ys) :-
        (
            foreach(X, Xs),
            foreach(Y, Ys),
            fromto(1, In, Out, 1)
        do
            In #= (X #< Y + Out)
        ).

    Which constraint does this code implement? (Hint: declaratively, it is the same as one of the constraints from ic_global, but is implemented somewhat differently.) How does it work?

Previous Up